Formula Special Considerations

Time of Day

For the purposes of the RealVol Real-Time Formula, the calculation of the number of seconds, s, within the current trading day does not necessarily start at the beginning of the day (midnight), but rather at the closing time of the market on the previous trading day. For example, the stock market in the U.S. closes at 4:00 PM Eastern Time (16:00  on  a 24-hour  clock).  Therefore, the  end of  the trading day is 4:00 PM and “tomorrow’s” trading day begins immediately afterwards.

If the current time is 7:00 PM (19:00), the current day’s second count is 10,800 (60 seconds per minute x 60 minutes per hour x 3 hours after the market’s close). To continue with this example, three hours is 3/24 (or 0.125 expressed as a decimal) of a whole day.  Similarly, 10,800 seconds is 10,800/86,400 (or the same 0.125 expressed as a decimal) of a whole day.

Note: It makes no difference if the market is indeed open 24 hours. If the market opens at, say, 9:30 AM (09:30) the following morning, this is 17.5 hours after the market closed on the previous day; thus, 17.5/24 hours, or 63,000/86,400 seconds, or 0.7292 weight for the current day’s (n+1) most recent return would be used in the calculation.

Non-Trading Days

Since there are weekends, holidays, and potential market disruption events that could occur, it is important to know how the calculation of the RealVol Indices will be affected by these non-trading, or partially trading, days.

1. In the case of a weekend day, there is no Underlying Reference Price (“URP”) or possible calculation of a return, so weekend days will be ignored. In essence, the close-to-close formula will continue as if the non-trading weekend days never existed. No RealVol Index will be calculated or disseminated on weekend days.
2. In the case of holidays, there is no URP or possible calculation of a return, so those days will be ignored. In essence, the close-to-close formula will continue as if the non-trading holiday never existed. No RealVol Index will be calculated or disseminated on holidays.
3. In the case of a partial day Market Disruption Event (MDE), please see the section entitled Process for Market Disruption Events.
4. If the MDE prevents the trading or calculation of any URP for the entire day, no return calculation is possible. However, the RVOL and RVOV Indices will continue to be calculated and published (if publication is possible). In order to keep the same rolling set of daily returns moving through time, the RVOL Indices cannot simply ignore the originally scheduled trading day that did not occur. Thus, it will use  the  same  set of data normally  scheduled for  the rolling 21-day, 63-day, and 252-day versions, but will compensate for the missing day’s returns by lowering the value of n by the full number of days of the  MDE.  See Exhibit 1 for a table outlining the day counts prior to, throughout, and after a full day’s MDE.

For example, if today is a scheduled trading day, but the market could not open, and hence the market could not close, the normal 21-day RVOL Index will be published as 20-day RVOL Index for the period during which the MDE coincides with the normal 21-day returns schedule.  In essence, the first day  will be  dropped as  we  perform  the normal roll process, but the 21st day will not be added because there is no URP available “today.” In the potential of an MDE that spans multiple days, such that neither the primary market nor any of the surrogate markets open, and hence cannot close, the algorithm will continue to reduce the number of days in the calculation period to as few as ten days for 1RVOL, 31 days for 3RVOL, and 126 days for 12RVOL (“Min Calculation Period”).

If, indeed, an MDE causes the underlying to lack pricing for less than the Min Calculation Period the RealVol Indices will remain the same until such time as the URPs are again available. Subsequent days will be added, but no days removed, until the Defined Days are restored to their full number of expected trading days. It should be noted that the MDE will continue to affect the calculation of VOL, RVOL, and RVOV Indices even after the MDE has passed (again, unless the Minimum Calculation Period has been exceeded). This is because every Realized Volatility calculation has a look-back period, and if that period coincides with the MDE, it will continue to affect the calculation in the same manner. For example, suppose that an MDE event occurred yesterday and the market opens normally today. All RealVol Indices will be calculated and disseminated for today’s normal trading day. However, the number of returns will be reduced by 1 until 20 days beyond the MDE day. Please see Exhibit 1 showing the value of n through time.

Exhibit 1

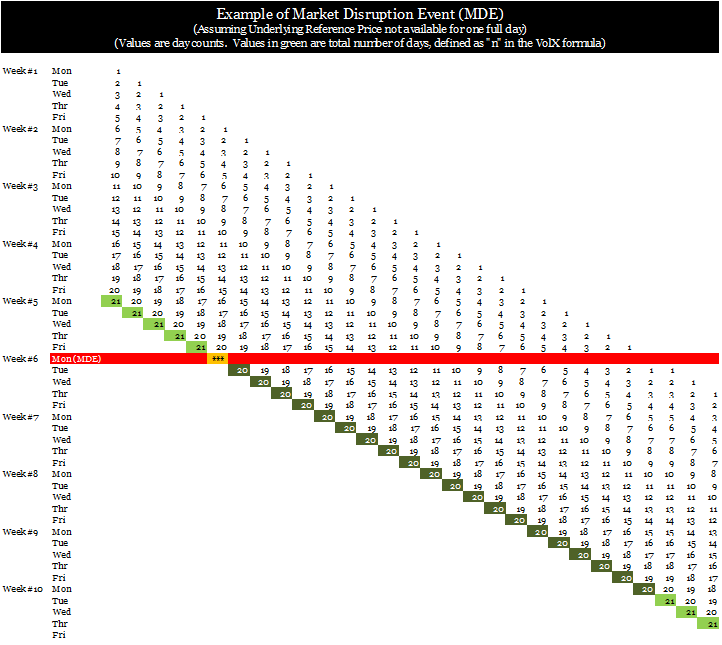
Notes

• An MDE day occurs when there is no published Underlying Reference Price. In the above example, the MDE occurs on Monday of Week #6.
• All RealVol Indices will be published on all normally scheduled trading days, even days where  the  underlying market does not open and hence does not close.
• All highlighted days (light green, orange, and dark green) are days where the RealVol Indices are published.
• The light green highlights indicate normal 21-trading-days of daily returns.
• The dark green highlights indicate a period of MDE with fewer than 21tradingdays of daily returns.
• The orange highlighted day indicates a day where the daily RVOL and RVOV indices will be published but where the underlying URP, and hence that daily return, will not.

Phantom Volatility

Now that the formula is defined, the URPs may need adjusting to remove any “contrived,” “artificial,” or “non-normal” volatility that may exist (collectively called “phantom volatility”). There are many examples of how such phantom volatility is possible.

Stocks Paying a Dividend

Many companies pay a dividend to holders of company stock. If such a stock were the underlying, and the company paid a dividend, typically its stock would drop by the value of the dividend on the ex-dividend day. This is rational because no value has been created by such an event. A dividend merely transfers value from the company to the shareholder. For example, a company worth $99 per share that pays a $1 dividend should be valued afterwards at $98 (assuming all other factors have remained unchanged). The shareholder still has $99 of value (the stock worth $98 plus $1 in cash). However, if one is measuring the day-to-day return of this stock for volatility calculation purposes, the stock price just dropped roughly 1%. If the formula for calculating realized volatility did not take such an artificial drop into account, the resulting volatility would be misleading.

Stock Splits, Reverse Splits, Stock Dividends

Another example of phantom volatility would be if the underlying were a stock and the company goes through a stock split, reverse split, or stock dividend (for simplicity, all will be referred to as a “stock split” as the concept is the same regardless). Assume that, in this case, the number of shares doubles. Such an action obviously increases the number of shares outstanding but should not affect the value of the company. This is because in order to keep  the value of the company a constant, the share price must drop in half to compensate. However, since realized volatility is based only on price changes, and since the price changed substantially (artificially dropped in half), the realized volatility of the stock would be increased to an artificially large value. If the formula for calculating realized volatility did not take such an artificial drop into account, the resulting volatility would be misleading.

Expiring Underlyings

If the underlying is an instrument that expires, such as a futures contract, there is an adjustment required in order not to introduce phantom volatility that is truly not present.

There comes a point in the life of a futures contract where the front-month contract expires. And, it is logical to assume that the previously deferred month, which now becomes the new front month, then becomes the contract upon which further returns are based. Futures contracts are, as their name implies, based on a prediction — a forecast of a future event. As such, their values are predicated upon many factors, and so it is natural to assume that when one futures contract expires, the next one, chronologically, which may not expire until one month, two months, or perhaps three months, later, may differ in price from the recently expired one. Clearly, when one endeavors to calculate the RealVol Indices based on an underlying, and that underlying is a futures contract, such a “jump” in successive URPs could be problematic. Consider the following.

Suppose that an underlying March futures contract has just expired at a price of 100. Suppose, further, that, at that very moment of expiration, the deferred underlying June contract is trading at 102. Finally, suppose that, in the next day’s trading, the underlying June futures contract remains unchanged and closes once again at 102. In the calculation of a continuing series of closing-settlement returns, one might use the underlying March contract until it stops trading. In this case, the final price is 100. For the next trading day, there is zero interday volatility, because the market is unchanged, and yet the new closing reference point would be 102 — that of the underlying June contract. In the calculation process, were one to simply “roll” the return calculation from underlying March into underlying June, there would be the appearance of a two-point jump in the reference prices, from 100 to 102, implying some daily realized volatility when, in fact, there is none.

A Deliverable Futures Contract as an Underlying

When the underlying is a deliverable commodity futures contract (instead of being cash settled), the roll from one contract to the next is performed early (rolling just prior to the delivery month).  This is done because the unfettered price discovery process can be adversely affected during the delivery process.  Hence, for many commodities and energy products, RealVol indices use pre-delivery rolls.

Short-Term Interest Rate Futures

When short-term rates approach zero, calculating returns can be problematic as denominators cannot be zero.  Therefore, the accepted method in the marketplace to address this concern is to use a normal distribution rather than a lognormal distribution when the interest rate is at or below 1.00%.   This corresponds to findings of several academic papers, which studied the issue.  It also corresponds to the accepted method found in the marketplace.

An Index as the Underlying

If the underlying is an index, no adjustments shall be made except if the index goes through a normalization event (i.e., the index is rebased).  Any treatment of dividends, or lack thereof, or the treatment of stock splits, stock dividends, etc., is in the domain of the company creating and calculating the index.  RealVol will not “look through” the index to the underlying stocks and eliminate any phantom volatility.  So, for example, if one wants information on the realized volatility of the S&P 500 with or without dividends, one could look to the RealVol Index on the S&P 500 Index or the S&P 500 Total Return Index as appropriate.

Adjusting for Phantom Volatility

Adjustment for Dividends

If the underlying is a security and the security pays a dividend, the security’s price needs to be adjusted to account for any dividend paid.  Therefore, to properly calculate realized volatility, subtract the dividend from the URP on the day prior to ex-dividend day before calculating a return for ex-dividend day.  The end result removes phantom volatility caused by a contrived situation of a paid dividend.  The day after ex-dividend day, the adjustment is not needed or carried through, and the calculation reverts to simply the return for the following day, using the unadjusted, actual URPs. 

To clarify:  An index is not a security.  Therefore, no adjustment for dividends shall pass through from the stocks that compose the index to the calculation of realized volatility.  For example, if one wanted the realized volatility of the S&P 500 index without adding back the dividends, one would simply use the index values as published each day by Standard and Poor’s.  If one wanted the realized volatility of the S&P 500 index with dividends reinvested, one would simply use the S&P 500 Total Return Index as the underlying.

Dividends

Normally, the closing price on any given day is the same as the URP.

P_t  = URP_t

In the event of a dividend paid on a security, the price used as the URP on the day prior to ex-dividend day (URPXDD-1) will be adjusted by the dividend payment as outlined in Formula 7.

Formula 7

P_t-1  = URP_XDD-1 + Dividend_XDD

Where:
XDD = Ex-dividend day
URP_XDD-1 = Underlying Reference Price on the day prior to ex-dividend day
Dividend_XDD  = The per-share declared dividend to be paid to shareholders of record on ex-dividend day.

Adjustment for Stock Splits

Stock splits, therefore, can introduce phantom volatility. To eliminate such phantom volatility, the daily or intraday return would be adjusted by multiplying the share price on its stock- split day by the ratio of the new number of shares divided by the original number of shares. For example, if the number of original shares was 1,000 and a stock split such that every share becomes two shares, the ratio is 2,000/1,000 = 2. Hence, the price on stock-split day would need to be multiplied by two as well in order to eliminate phantom volatility caused because of a stock split. The following day, the adjustment is not needed or carried through, and the calculation reverts to simply the return for the day, using the unadjusted, actual URPs.

Formula 8

P_t-1 = URP_XED-1 (Number of shares after split_XED-1 /Number of shares before split_XED)